之前讲过对称加密,比如DES, AES, 还有AES对应到的各种模式,比如ECB, CBC, CTR, GCM.
对称加密唯一保密的就是密钥(Key), 有了这个密码你就能解密其中的内容。
公开通信信道(Channel)
数字世界中的通信信道其实可以类比真实物理世界, 我们要从上海到北京就要经常各种各样的道路,比如走高速公路,就可能要经常各种检查站,收费站,理论上这些站点都可以对你的车进行全方位的搜索检查,看有没有携带违禁品。互联网世界一样,你的数据要经常中间的各种Wifi, 路由,网关,光纤,每个路由网关理论上都可以把你的传输数据拦截下来,甚至篡改,所以我们要知道公开的这些通信信道是不安全不可信任的。
所以想想我们的数据在这些不可信任的路途中穿梭还是挺可怕的。
动机(Motivation)
现在我们已经可以通过AES加密数据了,把加密的内容传输出去。但是密码要怎么传输出去了,因为密码是明文的,它在这些公开通信信息里面传输就一定会可能被黑客拦截到,还有一个问题,如果你一直用同一个密码,那么黑客就可以一直拦截你的信息,甚至在得到密码之前就一直在拦截,直到某一天得到密码了,那么黑客就可以同时解密之前已经存在很的加密信息了,如果密码不改,那将来的加密信息也一样会被黑客解密。
所以密码学科学家们绞尽脑汁想设计出来一种方法,可以解决在不安全信道中交互密钥的问题
于是就设计出了一种通过密钥对的加解密方式,同时生成一对密钥
- 私钥(Private Key) — 自己保留,绝对保密
- 公钥(Public Key) — 公开发布,分享给其它人
公钥加密,私钥解密。这样别人就可以拿到你的公钥把需要保密的信息进行加密发给你,你收到后通过私钥进行解密。
这个想法很奇妙,然后真的就做出来了。
RSA(Rivest, Shamir, Adleman)
RSA就是其中一种非对称加密算法,它就是可以生成一对公钥,私钥。可能大家以为这个是最近才发明的,但其实这个是很早就了1977年,RSA就发明了,一直用到现在。

它基于的数学原理其实很简单,简单到一个小学生都容易理解
- 大整数的因式分解
假设我们有两个质数p, q, N=p*q, 那当我们只知道N的时候是没办法算出p和q的,这个基本原理就是RSA的本质。
其实想想很简单,但总会觉得有点不可思议对吧,但现实就是这样,如果有谁能过够在只知道N的情况下算出p和q,那么RSA就完蛋了。
RSA的计算过程很简单
选择两个质数 p, q
N= p * q
Phi(N) = (p-1) * (q-1)
再选取一个e, 1<e<Phi(N),通常我们会选择e=65537
通过公式算出d, 满足条件 e * d mod Phi(N) = 1
这样就得到公钥Public Key(e, N), 私钥Private Key(d, N)当然实际的过程中这些数数会长,比如>1024,如下面这个是我从一个证书里面抓取到的。
p: 132069789892654411168004522386293936563648260984708049888769058861400033840104922637240827355145535778467721990046061228393420363010924409941513508800258809981119101399937003195217979917259199066675447728576676098948661691324234988484581514373041670098119069924124636404134462689209640493314790132976282083611
q: 137105056982080406391028823084893501194543535606308088202698272087931645688882684542797221955650442538986772234601648478841035329665841202081550877179575957078786677686845060335508172755008305533505548942627696405948787947081088462002379085459968945063951380151782547161878405562777603813013479678683689059989
e: 65537
d: 756214848412734766389636904239299485009061447036919688389891952047609574545734290864923373793452280368637781527992131423339716753716888185459331923714856645280928404198259347205993579213846803666627529909232828722879650374490951581311985882248017934718743944682742282487622451272419143686155769738092352440521581984122740725976684511860250924537999931049740452351974285438729683375867711220177807812280621918795246117514339543091408571088210170010573980132856774272424920513332731618240977627013497573799860486533079269798618961305686700083116612832032852006212842303481886949894366447734991011109426370041918678153
N: 18107436068843769961592120494384716970785115109411255249546345948609495318598388096607410722799226196024630722689083053376476074858729887106484558379430237472333286381418093839181293825698895861125235085005989001100242472266354948404984880805585806133599679175254980258454991811852588023295429551087087505259481055918651153874312403039948814343657680828818579172724766105080872512340183146177770234401565111928007670988819164086328954605138596051183819569014922240750776080760982732900349444868680946505230852975887754348080529969823222341004758720100799077687160346328480228883962117022614977552611965834106892740279
phi_N: 18107436068843769961592120494384716970785115109411255249546345948609495318598388096607410722799226196024630722689083053376476074858729887106484558379430237472333286381418093839181293825698895861125235085005989001100242472266354948404984880805585806133599679175254980258454991811852588023295429551087087505259211881071776419056753369694477626905899489032227563034633298774131540832811195538997732185090769133610553176764171454379094498912461830439160755183035087473690870301674200669369623292196413441905049856304683381843183080331417898890517798120267788462525089896252573045317949248770627733246283696022446921596680
RSA 加密是
𝑀^𝑒 𝑚𝑜𝑑 𝑁=𝐶解密是
𝐶^𝑑 𝑚𝑜𝑑 𝑁=𝑀其中M是明文,C是密文
针对RSA也有很多攻击方式,比如Timing-Attack against Square-&-Multiply
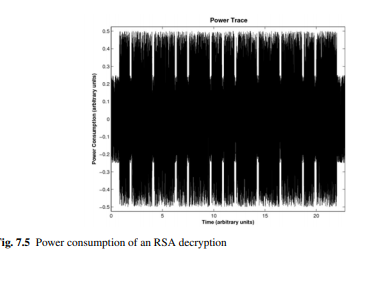
由于RSA的计算方式,使用了一种Square&Multiply的方式,在CPU运算时会有上图这种对应关系。
然后对Phi(N)也进行保密,不要复用N,每次都重新生成p, q等等。
如果消息长度过短也会出现问题
M=3,公钥(e=13, N=3000009)
加密=M^e mod 3000009 = 3^13 mod 3000009 = 1594323 mod 3000009 = 1594323 = 3^13 = M^e
所以最终只需要开根后就可以得到明文:3所以针对RSA加密有一条铁律,一定要使用OAEP(Optimal Asymmetric Encryption Padding)试对原明文进行padding
OAEP – Optimal Asymmetric Encryption Padding
OAEP本身只是加入了一种额外的Padding, 加了一些转换操作,这样在进行RSA加密前,先把明文M变成X,Y然后再加密,解密过程正好相反,这样因为有r(随机数)的存在,每次加密出的内容都是不一样的。
如下图


初次实现了非安全信道消息传递
再回到我们之前想传递一个通过AES密码加密的文件,现在我们可以通过RSA把密钥传送过来了。
有了RSA再加上对称加密AES,这样我们就可以第一次实现在非安全信道上的消息传递,我们把RSA公钥分发给对方,对方用RSA公钥把他的AES密码进行加密,这样我们就可以用我们的私钥解密得到这个文件的AES密码,然后就可以解密对应的文件了。
太不容易了,终于实现了第一次在非安全信息上的文件+密码传递。
数字签名(Digital Signatures)
其实我们看到RSA公钥可以分发出去,这样别人就可以用公钥加密发给你了,但有一个问题,每个人都可以通过这个公钥加密信息发给你,但你没办法区分到底是谁发的。
这样我们就要引入数字签名技术了
发送方先计算出文件的hash, 比如SHA256, 然后再用私钥进行签名hash^d mod N这里的签名要注意是用的用的对方自己的私钥,只有文件持有者才拥有的私用,别人只能有他的公钥。
这样对别上收到文件后,就可以用它的公钥进行验证
signature^e mod N = hash这样收件方通过计算文件的hash值,然后再通过比对这两个hash是否一样用来觉得这个内容是否被篡改过,还有是否是对方本人发的,因为私钥别人是没有的。
所以记住数字签名是,私钥签名,公钥验签,验证的是hash值。
很巧妙对吧,这些也不知道最早是谁想出来的,简直天才。
DH和FPS(Perfect Forward Secrecy)
虽然我们可以通过RSA生成密钥对,但我们不能每次都生成一个,因为公钥分发是有成功和时间的。如果我们一直用同一个RSA公租钥对,黑客可以一直抓取我们的密文,直到有一天,他得到了私租,那么我们之前所有的内容都会被解密,这是我们不希望看到的。
这个问题就可以叫做FPS(完美前向保密)。
所以为了解决这这个问题,科学家又发明了Diffie-Hellman(DH)密钥交换算法。
这个算法是基于离散对数难解的问题
g^x mod p = a这个离散对数问题是假设别人知道了g, p, a,它是很难计算出x。

通过共享g, p, 然后再分别选取私有的a, b, 计算出A, B分别共享给对方,得到A, B之后两个人再分别计算出共享密钥S, 下面这个公式推导就证明了两个人的密钥一致。
DH同样没有解决中间人攻击问题,所以还是要加上签名才能保证数据完整性,认证性。
ECC(Elliptic Curves, 椭圆曲线)
虽然我们已经有了RSA,但它的运算效率没有那么高,所以又有科学家基于椭圆曲线难解的问题,发明了另外一个公钥加密算法,最关键的是它的加密效率很高,运算速度高,只需要很短的密钥就能达到RSA 1024, 2048的保密效果。
所以ECC绝对是RSA替换首选,在一些嵌入式设备或者硬件性能没有那么好的设备上就可以使用ECC了,当然其它地方我觉得一样是推荐用ECC。
